Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 64, pp. 1-9.
A boundary blow-up for sub-linear elliptic problems with a
nonlinear gradient term
Zhijun Zhang
Abstract:
By a perturbation method and constructing comparison functions,
we show the exact asymptotic behaviour of solutions to
the semilinear elliptic problem

where
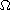 is a bounded domain in
is a bounded domain in
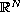 with smooth
boundary,
with smooth
boundary,
![$q\in (1, 2]$](gifs/ad.gif) ,
,
 ,
,
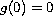 ,
,
 is increasing on
is increasing on
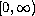 ,
and
,
and
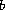 is non-negative non-trivial in
is non-negative non-trivial in
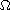 ,
which may be singular or vanishing on the boundary.
,
which may be singular or vanishing on the boundary.
Submitted February 5, 2006. Published May 20, 2006.
Math Subject Classifications: 35J60, 35B25, 35B50, 35R05.
Key Words: Semilinear elliptic equations; large solutions;
asymptotic behaviour.
Show me the
PDF file (225K),
TEX file, and other files for this article.
 |
Zhijun Zhang
Department of Mathematics and Information Science
Yantai University, Yantai, Shandong, 264005, China
email: zhangzj@ytu.edu.cn |
|---|
Return to the EJDE web page

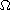 is a bounded domain in
is a bounded domain in
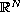 with smooth
boundary,
with smooth
boundary,
![$q\in (1, 2]$](gifs/ad.gif) ,
,
 ,
,
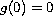 ,
,
 is increasing on
is increasing on
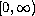 ,
and
,
and
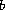 is non-negative non-trivial in
is non-negative non-trivial in
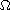 ,
which may be singular or vanishing on the boundary.
,
which may be singular or vanishing on the boundary.
