Giovany M. Figueiredo
Abstract:
This article concerns the
multiplicity of solutions for the system of equations
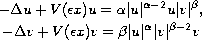
in
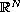 , where
, where
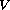 is a positive potential.
We relate the number of solutions with the topology of the set where
is a positive potential.
We relate the number of solutions with the topology of the set where
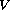 attains its minimum.
The results are proved by using minimax theorems and
Ljusternik-Schnirelmann theory.
attains its minimum.
The results are proved by using minimax theorems and
Ljusternik-Schnirelmann theory.
Submitted May 24, 2005. Published July 12, 2006.
Math Subject Classifications: 35J20, 35J50, 35J60.
Key Words: Variational methods; Palais-Smale condition;
Ljusternik-Schnirelmann theory.
Show me the PDF file (260K), TEX file for this article.
 |
Giovany M. Figueiredo Universidade Federal do Pará Departamento de Matemática CEP: 66075-110 Belém - Pa, Brazil email: giovany@ufpa.br |
|---|
Return to the EJDE web page