Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 01, pp. 1-7.
On oscillation and asymptotic behaviour of a neutral differential
equation of first order with positive and negative coefficients
Radhanath Rath, Prayag Prasad Mishra, Laxmi Narayan Padhy
Abstract:
In this paper sufficient conditions are obtained so that every
solution of
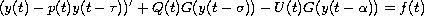
tends to zero or to
 as
as
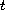 tends to
tends to
 , where
, where
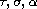 are positive real numbers,
are positive real numbers,
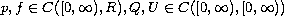 , and
, and
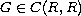 ,
,
 is non decreasing with
is non decreasing with
 for
for
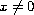 .
The two primary assumptions in this paper are
.
The two primary assumptions in this paper are
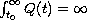 and
and
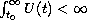 .
The results hold when
.
The results hold when
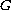 is linear, super linear,or sublinear and also hold when
is linear, super linear,or sublinear and also hold when
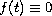 .
This paper generalizes and improves some
of the recent results in [5,7,8,10].
.
This paper generalizes and improves some
of the recent results in [5,7,8,10].
Submitted November 2, 2006. Published January 2, 2007
Math Subject Classifications: 34C10, 34C15, 34K40.
Key Words: Oscillatory solution; nonoscillatory solution;
asymptotic behaviour.
Show me the
PDF file (216K),
TEX file for this article.
 |
Radhanath Rath
Department of Mathematics
Khallikote Autonomous College
Berhampur, 760001 Orissa, India
email: radhanathmath@yahoo.co.in |
|---|
 |
Prayag Prasad Mishra
Department of Mathematics
Silicin Institute of Technology
Bhubaneswar, Orissa, India
email: prayag@silicon.ac.in |
|---|
 |
Laxmi Narayan Padhi
Department of Mathematics, K.I.S.T
Bhubaneswar Orissa, India
email: ln_padhy_2006@yahoo.co.in |
|---|
Return to the EJDE web page
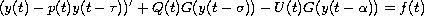
 as
as
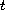 tends to
tends to
 , where
, where
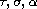 are positive real numbers,
are positive real numbers,
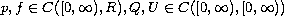 , and
, and
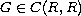 ,
,
 is non decreasing with
is non decreasing with
 for
for
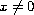 .
The two primary assumptions in this paper are
.
The two primary assumptions in this paper are
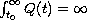 and
and
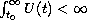 .
The results hold when
.
The results hold when
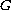 is linear, super linear,or sublinear and also hold when
is linear, super linear,or sublinear and also hold when
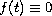 .
This paper generalizes and improves some
of the recent results in [5,7,8,10].
.
This paper generalizes and improves some
of the recent results in [5,7,8,10].


