We consider a numerical scheme for entropy weak solutions of the DP (Degasperis-Procesi) equation
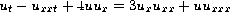 . Multi-shockpeakons,
functions of the form
. Multi-shockpeakons,
functions of the form
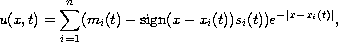
are solutions of the DP equation with a special property; their evolution in time is described by a dynamical system of ODEs. This property makes multi-shockpeakons relatively easy to simulate numerically. We prove that if we are given a non-negative initial function
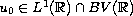 such that
such that
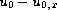 is a positive Radon measure, then one can
construct a sequence of multi-shockpeakons which converges to
the unique entropy weak solution in
is a positive Radon measure, then one can
construct a sequence of multi-shockpeakons which converges to
the unique entropy weak solution in
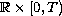 for any
for any
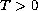 .
From this convergence result, we construct a multi-shockpeakon based
numerical scheme for solving the DP equation.
.
From this convergence result, we construct a multi-shockpeakon based
numerical scheme for solving the DP equation.
