In this paper we prove the exponential and polynomial decays rates in the case
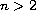 ,
as time approaches infinity of regular solutions
of the wave equations with memory
,
as time approaches infinity of regular solutions
of the wave equations with memory
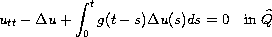
where
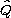 is a non cylindrical domains of
is a non cylindrical domains of
 ,
,
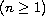 .
We show that the dissipation produced by memory effect is
strong enough to produce exponential decay of solution provided
the relaxation function
.
We show that the dissipation produced by memory effect is
strong enough to produce exponential decay of solution provided
the relaxation function
 also decays
exponentially. When the
relaxation function decay polynomially, we show that the solution
decays polynomially with the same rate. For this we introduced a
new multiplier that makes an important role in the obtaining of
the exponential and polynomial decays of the energy of the system.
Existence, uniqueness and regularity of solutions for any
also decays
exponentially. When the
relaxation function decay polynomially, we show that the solution
decays polynomially with the same rate. For this we introduced a
new multiplier that makes an important role in the obtaining of
the exponential and polynomial decays of the energy of the system.
Existence, uniqueness and regularity of solutions for any
 are investigated. The obtained result extends known
results from cylindrical to non-cylindrical domains.
are investigated. The obtained result extends known
results from cylindrical to non-cylindrical domains.
