This paper establishes a new criteria for obtaining a sequence of upper and lower bounds for the ground state eigenvalue of Schrodinger equation
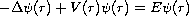in
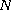spatial dimensions.
Based on this proposed criteria, we prove a new comparison theorem
in quantum mechanics for the ground state eigenfunctions of
Schrodinger equation. We determine also lower and upper
solutions for the exact wave function of the ground state
eigenfunctions using the computed upper and lower bounds for the
eigenvalues obtained by variational methods. In other words, by
using this criteria, we prove that the substitution of the
lower(upper) bound of the eigenvalue in Schrodinger equation
leads to an upper(lower) solution. Finally, two proposed iteration
approaches lead to an exact convergent sequence of solutions. The
first one uses Raielgh-Ritz theorem. Meanwhile, the second
approach uses a new numerical spectral bisection technique. We
apply our results for a wide class of potentials in quantum
mechanics such as sum of power-law potentials in quantum
mechanics.
