Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 173, pp. 1-8.
Application of Pettis integration to differential inclusions
with three-point boundary conditions in Banach spaces
Dalila Azzam-Laouir, Imen Boutana
Abstract:
This paper provide some applications of Pettis integration to differential
inclusions in Banach spaces with three point boundary conditions of the form
![$$
\ddot{u}(t) \in F(t,u(t),\dot u(t))+H(t,u(t),\dot u(t)),\quad
\hbox{a.e. } t \in [0,1],
$$](gifs/aa.gif)
where
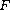 is a convex valued multifunction upper semicontinuous on
is a convex valued multifunction upper semicontinuous on
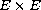 and
and
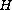 is a lower semicontinuous multifunction.
The existence of solutions is obtained under the non convexity condition
for the multifunction
is a lower semicontinuous multifunction.
The existence of solutions is obtained under the non convexity condition
for the multifunction
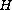 ,
and the assumption that
,
and the assumption that
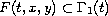 ,
,
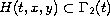 , where the multifunctions
, where the multifunctions
![$\Gamma_{1},\Gamma_{2}:[0,1]\rightrightarrows E$](gifs/ag.gif) are uniformly Pettis integrable.
are uniformly Pettis integrable.
Submitted September 5, 2007. Published December 6, 2007.
Math Subject Classifications: 34A60, 28A25, 28C20.
Key Words: Differential inclusions; Pettis-integration; selections.
An addendum was posted on September 15, 2016.
It states a correction needed in Proposition 3.3.
See the last page of this article.
Show me the
PDF file (231 KB),
TEX file, and other files for this article.
Dalila Azzam-Laouir
Laboratoire de Mathématiques Pures
et Appliquées
Université de Jijel, Algérie
email: azzam_d@yahoo.com |
Imen Boutana
Laboratoire de Mathématiques Pures
et Appliquées
Université de Jijel, Algérie
email: bou.imend@yahoo.fr |
Return to the EJDE web page
![$$
\ddot{u}(t) \in F(t,u(t),\dot u(t))+H(t,u(t),\dot u(t)),\quad
\hbox{a.e. } t \in [0,1],
$$](gifs/aa.gif)
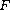 is a convex valued multifunction upper semicontinuous on
is a convex valued multifunction upper semicontinuous on
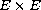 and
and
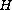 is a lower semicontinuous multifunction.
The existence of solutions is obtained under the non convexity condition
for the multifunction
is a lower semicontinuous multifunction.
The existence of solutions is obtained under the non convexity condition
for the multifunction
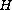 ,
and the assumption that
,
and the assumption that
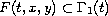 ,
,
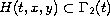 , where the multifunctions
, where the multifunctions
![$\Gamma_{1},\Gamma_{2}:[0,1]\rightrightarrows E$](gifs/ag.gif) are uniformly Pettis integrable.
are uniformly Pettis integrable.