Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 31, pp. 1-10.
On a convex combination of solutions to elliptic variational
inequalities
Mahdi Boukrouche, Domingo A. Tarzia
Abstract:
Let
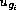 the unique solutions of an elliptic
variational inequality with second member
the unique solutions of an elliptic
variational inequality with second member
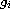 (
(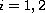 ).
We establish necessary and sufficient conditions for the convex
combination
).
We establish necessary and sufficient conditions for the convex
combination
 , to be equal to
the unique solution of the same elliptic variational inequality
with second member
, to be equal to
the unique solution of the same elliptic variational inequality
with second member
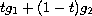 .
We also give some examples where this property is valid.
.
We also give some examples where this property is valid.
Submitted September 15, 2006. Published February 22, 2007.
Math Subject Classifications: 35R35.
Key Words: Elliptic variational inequalities;
convex combination of its solutions.
Show me the
PDF file (213K),
TEX file for this article.
 |
Mahdi Boukrouche
Laboratory of Mathematics, University of Saint-Etienne
23 rue du Dr Paul Michelon
Saint-Etienne, 42023, France
Phone: 33 4 77 48 15 35; fax: 33 4 77 25 60 71
email: Mahdi.Boukrouche@univ-st-etienne.fr |
|---|
 |
Domingo A. Tarzia
Departamento Matemática - CONICET
FCE, Univ. Austral
Paraguay 1950, S2000FZF Rosario, Argentina
email: Domingo.Tarzia@fce.austral.edu.ar |
|---|
Return to the EJDE web page
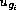 the unique solutions of an elliptic
variational inequality with second member
the unique solutions of an elliptic
variational inequality with second member
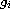 (
(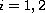 ).
We establish necessary and sufficient conditions for the convex
combination
).
We establish necessary and sufficient conditions for the convex
combination
 , to be equal to
the unique solution of the same elliptic variational inequality
with second member
, to be equal to
the unique solution of the same elliptic variational inequality
with second member
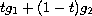 .
We also give some examples where this property is valid.
.
We also give some examples where this property is valid.

