Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 37, pp. 1-21.
On a class of nonlinear variational inequalities:
High concentration of the graph of weak solution via its
fractional dimension and Minkowski content
Luka Korkut, Mervan Pasic
Abstract:
Weak continuous bounded solutions of a class of nonlinear
variational inequalities associated to one-dimensional
p-Laplacian are studied. It is shown that a kind of boundary
behaviour of nonlinearity in the main problem produces a kind of
high boundary concentration of the graph of solutions. It is
verified by calculating lower bounds for the upper
Minkowski-Bouligand dimension and Minkowski content of the graph
of each solution and its derivative. Finally, the order of growth
for singular behaviour of the
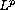 norm of derivative of
solutions is given.
norm of derivative of
solutions is given.
Submitted November 19, 2006. Published March 1, 2007.
Math Subject Classifications: 35J85, 34B15, 28A75.
Key Words: Double obstacles; nonlinear p-Laplacian; graph;
fractional dimension; Minkowski content;
singularity of derivative.
Show me the
PDF file (347K),
TEX file, and other files for this article.
| |
Luka Korkut
Department of mathematics
Faculty of Electrical Engineering and Computing
University of Zagreb
Unska 3, 10000 Zagreb, Croatia
e-mail: luka.korkut@fer.hr |
|---|
 |
Mervan Pasic
Department of mathematics
Faculty of Electrical Engineering and Computing
University of Zagreb
Unska 3, 10000 Zagreb, Croatia
e-mail: mervan.pasic@fer.hr |
|---|
Return to the EJDE web page
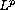 norm of derivative of
solutions is given.
norm of derivative of
solutions is given.
