Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 39, pp. 1-23.
Existence and uniqueness of global solutions
to a model for the flow of an incompressible,
barotropic fluid with capillary effects
Diane L. Denny
Abstract:
We study the initial-value problem for a system of nonlinear
equations that models the flow of an inviscid, incompressible,
barotropic fluid with capillary stress effects. We prove the
global-in-time existence of a unique, classical solution to this
system of equations, with a small initial velocity gradient. The
key to the proof lies in using an
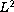 estimate for the density
estimate for the density
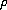 ,
and using the smallness of the initial velocity gradient,
to obtain uniqueness for the density.
,
and using the smallness of the initial velocity gradient,
to obtain uniqueness for the density.
Submitted August 10, 2006. Published March 6, 2007.
Math Subject Classifications: 35A05.
Key Words: Existence; uniqueness; capillary; incompressible;
inviscid fluid.
Show me the
PDF file (324K),
TEX file for this article.
 |
Diane Denny
Department of Mathematics and Statistics
Texas A&M University - Corpus Christi
Corpus Christi, TX 78412, USA
email: diane.denny@tamucc.edu |
|---|
Return to the EJDE web page
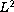 estimate for the density
estimate for the density
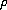 ,
and using the smallness of the initial velocity gradient,
to obtain uniqueness for the density.
,
and using the smallness of the initial velocity gradient,
to obtain uniqueness for the density.
