We prove the existence of bounded solutions for the nonlinear elliptic problem

with
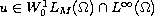 ,
where
,
where
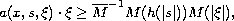
and
![$h:{\mathbb{R}^+}{\to }{]0,1]}$](gifs/ad.gif) is a continuous monotone
decreasing function with unbounded primitive.
As regards the
is a continuous monotone
decreasing function with unbounded primitive.
As regards the
 -function
-function
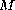 , no
, no
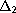 -condition
is needed.
-condition
is needed.
Ahmed Youssfi
Abstract:
We prove the existence of bounded solutions for the
nonlinear elliptic problem

with
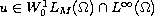 ,
where
,
where
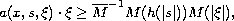
and
![$h:{\mathbb{R}^+}{\to }{]0,1]}$](gifs/ad.gif) is a continuous monotone
decreasing function with unbounded primitive.
As regards the
is a continuous monotone
decreasing function with unbounded primitive.
As regards the
 -function
-function
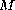 , no
, no
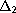 -condition
is needed.
-condition
is needed.
Submitted December 11, 2006. Published April 10, 2007.
Math Subject Classifications: 46E30, 35J70, 35J60.
Key Words: Orlicz-Sobolev spaces; degenerate coercivity;
L-infity-estimates; rearrangements.
Show me the PDF file (264K), TEX file for this article.
 |
Ahmed Youssfi Department of Mathematics and Informatics Faculty of Sciences Dhar El Mahraz University Sidi Mohammed Ben Abdallah PB 1796 Fez-Atlas, Fez, Morocco email: Ahmed.youssfi@caramail.com |
|---|
Return to the EJDE web page