Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 86, pp. 1-14.
Bernstein approximations of Dirichlet problems for
elliptic operators on the plane
Jacek Gulgowski
Abstract:
We study the finitely dimensional approximations of the elliptic problem
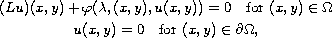
defined for a smooth bounded domain
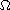 on a plane.
The approximations are derived from Bernstein polynomials on a triangle or
on a rectangle containing
on a plane.
The approximations are derived from Bernstein polynomials on a triangle or
on a rectangle containing
 .
We deal with approximations of
global bifurcation branches of nontrivial solutions
as well as certain existence facts.
.
We deal with approximations of
global bifurcation branches of nontrivial solutions
as well as certain existence facts.
Submitted January 2, 2007. Published June 14, 2007.
Math Subject Classifications: 35J25, 41A10.
Key Words: Dirichlet problems; Bernstein polynomials; global bifurcation.
Show me the
PDF file (266K),
TEX file for this article.
Jacek Gulgowski
Institute of Mathematics,
University of Gdansk
ul. Wita Stwosza 57, 80-952 Gdansk, Poland
email: dzak@math.univ.gda.pl
|
Return to the EJDE web page
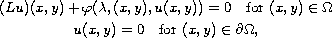
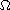 on a plane.
The approximations are derived from Bernstein polynomials on a triangle or
on a rectangle containing
on a plane.
The approximations are derived from Bernstein polynomials on a triangle or
on a rectangle containing
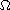 .
We deal with approximations of
global bifurcation branches of nontrivial solutions
as well as certain existence facts.
.
We deal with approximations of
global bifurcation branches of nontrivial solutions
as well as certain existence facts.