Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 92, pp. 1-9.
Continuous dependence for the Brinkman equations
of flow in double-diffusive convection
Hongliang Tu, Changhao Lin
Abstract:
This paper concerns the structural stability for
convective motion in a fluid-saturated porous medium
under the Brinkman scheme. Continuous dependence for the
solutions on the gravity coefficients and the Soret coefficient
are proved. First of all, an a priori bound in
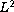 norm is derived whereby we show the solution depends
continuously in L^2 norm on changes in the gravity coefficients
and the Soret coefficient. This estimate also implies that the solutions
decay exponentially.
norm is derived whereby we show the solution depends
continuously in L^2 norm on changes in the gravity coefficients
and the Soret coefficient. This estimate also implies that the solutions
decay exponentially.
Submitted April 9, 2007. Published June 16, 2007.
Math Subject Classifications: 35B30, 35K55, 35Q35.
Key Words: Continuous dependence; structural stability;
gravity coefficients; Soret coefficient; Brinkman equations
Show me the
PDF file (196K),
TEX file for this article.
 |
Hongliang Tu
Department of Applied Mathematics
Zhuhai college of Jilin University, 519041, China
email: tuhongliang00@126.com
|
|---|
 |
Changhao Lin
School of Mathematical Sciences
South China Normal University, 510631, China
email: linchh@scnu.edu.cn
|
|---|
Return to the EJDE web page
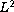 norm is derived whereby we show the solution depends
continuously in L^2 norm on changes in the gravity coefficients
and the Soret coefficient. This estimate also implies that the solutions
decay exponentially.
norm is derived whereby we show the solution depends
continuously in L^2 norm on changes in the gravity coefficients
and the Soret coefficient. This estimate also implies that the solutions
decay exponentially.

