Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 01, pp. 1-15.
Well-posedness and ill-posedness of the fifth-order
modified KdV equation
Soonsik Kwon
Abstract:
We consider the initial value problem of the fifth-order modified
KdV equation on the Sobolev spaces.
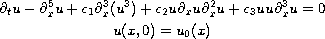
where
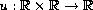 and
and
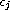 's
are real. We show the local well-posedness in
's
are real. We show the local well-posedness in
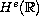 for
for
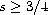 via the contraction principle on
via the contraction principle on
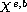 space. Also, we show that the solution map from data to the
solutions fails to be uniformly continuous below
space. Also, we show that the solution map from data to the
solutions fails to be uniformly continuous below
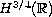 . The counter example is obtained by
approximating the fifth order mKdV equation by the cubic NLS
equation.
. The counter example is obtained by
approximating the fifth order mKdV equation by the cubic NLS
equation.
Submitted November 7, 2007. Published January 2, 2008.
Math Subject Classifications: 35Q53.
Key Words: Local well-posedness; ill-posedness; mKdV hierarchy.
Show me the
PDF file (297 KB),
TEX file for this article.
 |
Soonsik Kwon
Department of Mathematics, University of California
Los Angeles, CA 90095-1555, USA
email: rhex2@math.ucla.edu
|
|---|
Return to the EJDE web page
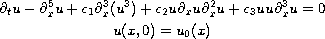
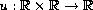 and
and
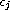 's
are real. We show the local well-posedness in
's
are real. We show the local well-posedness in
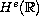 for
for
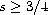 via the contraction principle on
via the contraction principle on
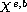 space. Also, we show that the solution map from data to the
solutions fails to be uniformly continuous below
space. Also, we show that the solution map from data to the
solutions fails to be uniformly continuous below
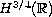 . The counter example is obtained by
approximating the fifth order mKdV equation by the cubic NLS
equation.
. The counter example is obtained by
approximating the fifth order mKdV equation by the cubic NLS
equation.
