Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 05, pp. 1-21.
Multiple solutions to a singular Lane-Emden-Fowler equation
with convection term
Carlos C. Aranda, Enrique Lami Dozo
Abstract:
This article concerns the existence of multiple
solutions for the problem
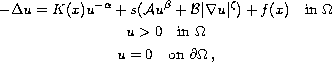
where
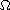 is a smooth, bounded domain in
is a smooth, bounded domain in
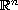 with
with
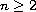 ,
,
 ,
,
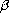 ,
,
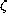 ,
,
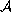 ,
,
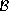 and
and
 are real positive numbers, and
are real positive numbers, and
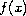 is a
positive real valued and measurable function. We start with the
case
is a
positive real valued and measurable function. We start with the
case
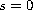 and
and
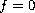 by studying the structure of the range of
by studying the structure of the range of
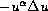 . Our method to build
. Our method to build
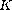 's
which give at least
two solutions is based on positive and negative principal
eigenvalues with weight. For
's
which give at least
two solutions is based on positive and negative principal
eigenvalues with weight. For
 small positive and for values
of the parameters in finite intervals, we find
multiplicity via estimates on the bifurcation set.
small positive and for values
of the parameters in finite intervals, we find
multiplicity via estimates on the bifurcation set.
Submitted August 12, 2007. Published January 2, 2008.
Math Subject Classifications: 35J25, 35J60.
Key Words: Bifurcation; weighted principal eigenvalues and eigenfunctions.
Show me the
PDF file (333 KB),
TEX file for this article.
 |
Carlos C. Aranda
Mathematics Department
Universidad Nacional de Formosa, Argentina
email: carloscesar.aranda@gmail.com
|
|---|
 |
Enrique Lami Dozo
CONICET-Universidad de Buenos Aires, Argentina.
and Univ. Libre de Bruxelles, Belgium
email: lamidozo@ulb.ac.be
|
|---|
Return to the EJDE web page
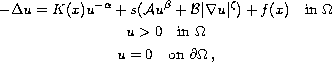
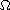 is a smooth, bounded domain in
is a smooth, bounded domain in
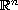 with
with
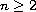 ,
,
 ,
,
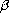 ,
,
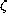 ,
,
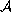 ,
,
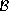 and
and
 are real positive numbers, and
are real positive numbers, and
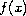 is a
positive real valued and measurable function. We start with the
case
is a
positive real valued and measurable function. We start with the
case
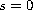 and
and
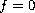 by studying the structure of the range of
by studying the structure of the range of
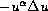 . Our method to build
. Our method to build
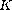 's
which give at least
two solutions is based on positive and negative principal
eigenvalues with weight. For
's
which give at least
two solutions is based on positive and negative principal
eigenvalues with weight. For
 small positive and for values
of the parameters in finite intervals, we find
multiplicity via estimates on the bifurcation set.
small positive and for values
of the parameters in finite intervals, we find
multiplicity via estimates on the bifurcation set.

