Electron. J. Diff. Eqns., Vol. 2008(2008), No. 109, pp. 1-22.

Energy decay for wave equations of $\phi$-Laplacian type with weakly nonlinear dissipation

Abbes Benaissa, Aissa Guesmia

Abstract:
In this paper, first we prove the existence of global solutions in Sobolev spaces for the initial boundary value problem of the wave equation of $\phi$-Laplacian with a general dissipation of the form
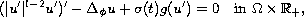
$$ (|u'|^{l-2}u')'-\Delta_{\phi}u+\sigma(t) g(u')=0 \quad\hbox{in } \Omega\times \mathbb{R}_+ , $$
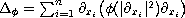where $\Delta_{\phi}=\sum_{i=1}^n \partial_{x_i}\bigl(\phi (|\partial_{x_i}|^2)\partial_{x_i}\bigr)$. Then we prove general stability estimates using multiplier method and general weighted integral inequalities proved by the second author in [18]. Without imposing any growth condition at the origin on $g$ and $\phi$, we show that the energy of the system is bounded above by a quantity, depending on $\phi$, $\sigma$ and $g$, which tends to zero (as time approaches infinity). These estimates allows us to consider large class of functions $g$ and $\phi$ with general growth at the origin. We give some examples to illustrate how to derive from our general estimates the polynomial, exponential or logarithmic decay. The results of this paper improve and generalize many existing results in the literature, and generate some interesting open problems.

Submitted September 19, 2007. Published August 11, 2008.
Math Subject Classifications: 35B40, 35L70.
Key Words: Wave equation; global existence; general dissipative term; rate of decay; multiplier method; integral inequalities.

Show me the PDF file (332 KB), TEX file, and other files for this article.

Abbes Benaissa
Department of Mathematics, Djillali Liabes University
P. O. Box 89, Sidi Bel Abbes 22000, Algeria
email: benaissa_abbes@yahoo.com
Aissa Guesmia
LMAM, ISGMP, Bat. A, UFR MIM, Université Paul Verlaine - Metz
Ile du Saulcy, 57045 Metz Cedex 01, France
email: guesmia@univ-metz.fr

Return to the EJDE web page