Electron. J. Diff. Eqns., Vol. 2008(2008), No. 111, pp. 1-11.

Positive solutions for an m-point boundary-value problem

Le Xuan Truong, Le Thi Phuong Ngoc, Nguyen Thanh Long

Abstract:
In this paper, we obtain sufficient conditions for the existence of a positive solution, and infinitely many positive solutions, of the m-point boundary-value problem
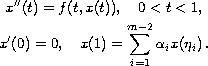
$$\displaylines{ x''(t) = f(t, x(t)), \quad 0 < t < 1, \cr x'(0) = 0, \quad x(1)=\sum_{i=1}^{m-2}\alpha _{i}x(\eta _{i})\,. }$$
Our main tools are the Guo-Krasnoselskii's fixed point theorem and the monotone iterative technique. We also show that the set of positive solutions is compact.

Submitted April 22, 2008. Published August 15, 2008.
Math Subject Classifications: 34B07, 34B10, 34B18, 34B27.
Key Words: Multi-point boundary; positive solution; Guo-Krasnoselskii fixed point theorem.

Show me the PDF file (240 KB), TEX file, and other files for this article.

Le Xuan Truong
University of Technical Education in HoChiMinh City 01 Vo Van Ngan Str., Thu Duc Dist.,
HoChiMinh City, Vietnam
email: lxuantruong@gmail.com
Le Thi Phuong Ngoc
Nhatrang Educational College, 01 Nguyen Chanh Str. Nhatrang City, Vietnam
email: ngoc1966@gmail.com
Nguyen Thanh Long
Department of Mathematics and Computer Science
University of Natural Science, Vietnam National University HoChiMinh City
227 Nguyen Van Cu Str., Dist. 5, HoChiMinh City, Vietnam
email: longnt@hcmc.netnam.vn, longnt2@gmail.com

Return to the EJDE web page