Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 114, pp. 1-10.
Existence of positive solutions for semipositone
dynamic system on time scales
Na-Na Shao, You-Wei Zhang
Abstract:
In this paper, we study the following semipositone
dynamic system on time scales
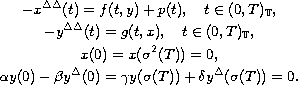
Using fixed point index theory, we show the existence of at
least one positive solution. The interesting point is the
that nonlinear term is allowed to change sign and may tend to
negative infinity.
Submitted April 8, 2008. Published August 20, 2008.
Math Subject Classifications: 34B15, 39A10
Key Words: Positive solution; semipositone dynamic system;
cone; fixed point index; time scales.
Show me the
PDF file (213 KB),
TEX file for this article.
 |
Na-Na Shao
School of Mathematics and Statistics, Lanzhou University
Lanzhou, 730000, Gansu, China
email: shaonn06@lzu.cn
|
|---|
| |
You-Wei Zhang
Department of Mathematics, Hexi University
Zhangye, 734000, Gansu, China
email: zhangyw05@lzu.cn
|
|---|
Return to the EJDE web page