Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 116, pp. 1-20.
Positive solutions for singular three-point
boundary-value problems
Ravi P. Agarwal, Donal O'Regan, Baoqiang Yan
Abstract:
Using the theory of fixed point index, this paper discusses the
existence of at least one positive solution and the existence
of multiple positive solutions for the singular three-point
boundary value problem:
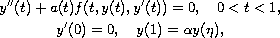
where
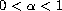 ,
,
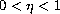 , and
, and
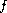 may be singular at
may be singular at
 and
and
 .
.
Submitted January 17, 2008. Published August 25, 2008.
Math Subject Classifications: 34B15.
Key Words: Three-point boundary value problems; singularity;
positive solutions; fixed point index.
Show me the
PDF file (282 KB),
TEX file, and other files for this article.
 |
Ravi P. Agarwal
Department of Mathematical Science
Florida Institute of Technology
Melbourne, Florida 32901, USA
email: agarwal@fit.edu |
|---|
 |
Donal O'Regan
Department of Mathematics, National University of Ireland
Galway, Ireland
email: donal.oregan@nuigalway.ie |
|---|
| |
Baoqiang Yan
Department of Mathematics, Shandong Normal University
Ji-nan, 250014, China
email: yanbqcn@yahoo.com.cn |
|---|
Return to the EJDE web page
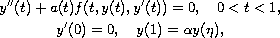
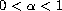 ,
,
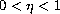 , and
, and
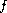 may be singular at
may be singular at
 and
and
 .
.

