Electron. J. Diff. Eqns., Vol. 2008(2008), No. 117, pp. 1-9.

An application of a global bifurcation theorem to the existence of solutions for integral inclusions

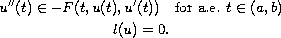
Stanislaw Domachowski

Abstract:
We prove the existence of solutions to Hammerstein integral inclusions of weakly completely continuous type. As a consequence we obtain an existence theorem for differential inclusions, with Sturm-Liouville boundary conditions,
$$\displaylines{ u''(t) \in -F(t,u(t),u'(t)) \quad\hbox{for a.e. } t\in(a,b) \cr l(u) = 0. }$$

Submitted April 17, 2008. Published August 25, 2008.
Math Subject Classifications: 47H04, 34A60, 34B24.
Key Words: Integral inclusion; differential inclusion; global bifurcation; selectors; Sturm-Liouville boundary conditions.

Show me the PDF file (234 KB), TEX file for this article.

Stanislaw Domachowski
Institute of Mathematics
University of Gdansk
ul. Wita Stwosza 57, 80-952 Gdansk, Poland
email: mdom@math.univ.gda.pl

Return to the EJDE web page