Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 125, pp. 1-9.
Existence of solutions to third-order m-point boundary-value problems
Jian-Ping Sun, Hai-E Zhang
Abstract:
This paper concerns the third-order m-point boundary-value problem
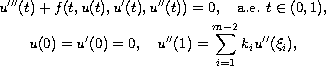
where
![$f:[0,1]\times \mathbb{R}^{3}\to \mathbb{R}$](gifs/ab.gif) is
is
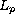 -Caratheodory,
-Caratheodory,
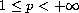 ,
,
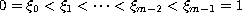 ,
,
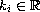 (
(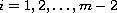 )
and
)
and
 .
Some criteria for the existence of at least one solution are
established by using the well-known Leray-Schauder Continuation Principle.
.
Some criteria for the existence of at least one solution are
established by using the well-known Leray-Schauder Continuation Principle.
Submitted March 25, 2008. Published September 4, 2008.
Math Subject Classifications: 34B10, 34B15.
Key Words: Third-order m-point boundary-value problem; Caratheodory;
Leray-Schauder continuation principle.
Show me the
PDF file (216 KB),
TEX file for this article.
 |
Jian-Ping Sun
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu, 730050, China
email: jpsun@lut.cn |
|---|
 |
Hai-E Zhang
Department of Basic Teaching, Tangshan College
Tangshan, Hebei 063000, China
email: ninthsister@tom.com
|
|---|
Return to the EJDE web page
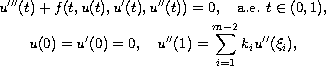
![$f:[0,1]\times \mathbb{R}^{3}\to \mathbb{R}$](gifs/ab.gif) is
is
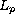 -Caratheodory,
-Caratheodory,
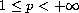 ,
,
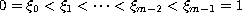 ,
,
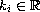 (
(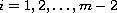 )
and
)
and
 .
Some criteria for the existence of at least one solution are
established by using the well-known Leray-Schauder Continuation Principle.
.
Some criteria for the existence of at least one solution are
established by using the well-known Leray-Schauder Continuation Principle.

