Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 132, pp. 1-10.
Large time behavior for solutions of nonlinear parabolic problems
with sign-changing measure data
Francesco Petitta
Abstract:
Let
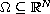 a bounded open set,
a bounded open set,
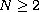 ,
and let
,
and let
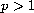 ;
in this paper we study the asymptotic behavior with
respect to the time variable
;
in this paper we study the asymptotic behavior with
respect to the time variable
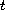 of the entropy solution of
nonlinear parabolic problems whose model is
of the entropy solution of
nonlinear parabolic problems whose model is
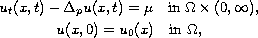
where
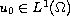 , and
, and
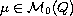 is
a measure with bounded variation over
is
a measure with bounded variation over
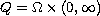 which does not charge the sets of zero
which does not charge the sets of zero
 -capacity; moreover we
consider
-capacity; moreover we
consider
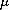 that does not depend on time. In particular, we
prove that solutions of such problems converge to stationary
solutions.
that does not depend on time. In particular, we
prove that solutions of such problems converge to stationary
solutions.
Submitted June 13, 2008. Published September 23, 2008.
Math Subject Classifications: 35B40, 35K55.
Key Words: Asymptotic behavior; nonlinear parabolic equations;
measure data.
Show me the
PDF file (233 KB),
TEX file for this article.
 |
Francesco Petitta
CMA, University of Oslo,
P.O. Box 1053 Blindern, NO-0316 Oslo, Norway
email: francesco.petitta@cma.uio.no
|
|---|
Return to the EJDE web page
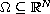 a bounded open set,
a bounded open set,
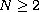 ,
and let
,
and let
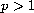 ;
in this paper we study the asymptotic behavior with
respect to the time variable
;
in this paper we study the asymptotic behavior with
respect to the time variable
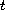 of the entropy solution of
nonlinear parabolic problems whose model is
of the entropy solution of
nonlinear parabolic problems whose model is
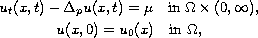
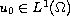 , and
, and
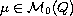 is
a measure with bounded variation over
is
a measure with bounded variation over
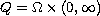 which does not charge the sets of zero
which does not charge the sets of zero
 -capacity; moreover we
consider
-capacity; moreover we
consider
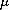 that does not depend on time. In particular, we
prove that solutions of such problems converge to stationary
solutions.
that does not depend on time. In particular, we
prove that solutions of such problems converge to stationary
solutions.
