Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 143, pp. 1-18.
Generalized eigenfunctions of relativistic Schrodinger operators
in two dimensions
Tomio Umeda, Dabi Wei
Abstract:
This article concerns the generalized eigenfunctions of the two-dimensional
relativistic Schrodinger operator
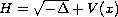 with
with
 ,
,
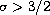 .
We compute the integral kernels of the boundary values
.
We compute the integral kernels of the boundary values
 ,
and
prove that the generalized eigenfunctions
,
and
prove that the generalized eigenfunctions
 are bounded on
are bounded on
 ,
where
,
where
![$[a,b]\subset(0,\infty)\backslash\sigma_p(H)$](gifs/ag.gif) ,
and
,
and
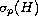 is the set of eigenvalues of
is the set of eigenvalues of
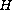 .
With this fact and the
completeness of the wave operators, we establish the eigenfunction
expansion for the absolutely continuous subspace for
.
With this fact and the
completeness of the wave operators, we establish the eigenfunction
expansion for the absolutely continuous subspace for
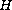 . Finally,
we show that each generalized eigenfunction is asymptotically
equal to a sum of a plane wave and a spherical wave
under the assumption that
. Finally,
we show that each generalized eigenfunction is asymptotically
equal to a sum of a plane wave and a spherical wave
under the assumption that
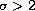 .
.
Submitted August 19, 2008. Published October 24, 2008.
Math Subject Classifications: 35P10, 81U05, 47A40.
Key Words: Relativistic Schrodinger operators; generalized eigenfunctions;
pseudo-relativistic Hamiltonians.
Show me the
PDF file (327 KB),
TEX file for this article.
 |
Tomio Umeda
Department of Mathematical Science,
University of Hyogo
Shosha 2167, Himeji 671-2201, Japan
email: umeda@sci.u-hyogo.ac.jp
|
|---|
 |
Dabi Wei
Department of Mechanical and Control Engineering
Graduate School of Science and Engineering
Tokyo Institute of Technology
2-12-1 S5-22 O-okayama, Meguro-ku, Tokyo 152-8550, Japan
email: dabi@ok.ctrl.titech.ac.jp
|
|---|
Return to the EJDE web page
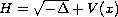 with
with
 ,
,
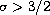 .
We compute the integral kernels of the boundary values
.
We compute the integral kernels of the boundary values
 ,
and
prove that the generalized eigenfunctions
,
and
prove that the generalized eigenfunctions
 are bounded on
are bounded on
 ,
where
,
where
![$[a,b]\subset(0,\infty)\backslash\sigma_p(H)$](gifs/ag.gif) ,
and
,
and
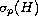 is the set of eigenvalues of
is the set of eigenvalues of
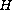 .
With this fact and the
completeness of the wave operators, we establish the eigenfunction
expansion for the absolutely continuous subspace for
.
With this fact and the
completeness of the wave operators, we establish the eigenfunction
expansion for the absolutely continuous subspace for
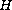 . Finally,
we show that each generalized eigenfunction is asymptotically
equal to a sum of a plane wave and a spherical wave
under the assumption that
. Finally,
we show that each generalized eigenfunction is asymptotically
equal to a sum of a plane wave and a spherical wave
under the assumption that
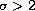 .
.

