Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 15, pp. 1-38.
Asymptotic behavior for a quadratic nonlinear
Schrodinger equation
Nakao Hayashi, Pavel I. Naumkin
Abstract:
We study the initial-value problem for the quadratic nonlinear
Schrodinger equation
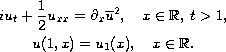
For small initial data
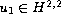 we prove
that there exists a unique global solution
we prove
that there exists a unique global solution
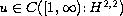 of this Cauchy
problem. Moreover we show that the large time asymptotic behavior
of the solution is defined in the region
of this Cauchy
problem. Moreover we show that the large time asymptotic behavior
of the solution is defined in the region
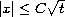 by the self-similar solution
by the self-similar solution
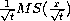 such that the total mass
such that the total mass
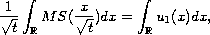
and in the far region
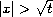 the asymptotic behavior of
solutions has rapidly oscillating structure similar to that of the cubic
nonlinear Schrodinger equations.
the asymptotic behavior of
solutions has rapidly oscillating structure similar to that of the cubic
nonlinear Schrodinger equations.
Submitted March 19, 2007. Published February 1, 2008.
Math Subject Classifications: 35B40, 35Q55.
Key Words: Nonlinear Schrodinger equation; large time asymptotic;
self-similar solutions.
Show me the
PDF file (433 KB),
TEX file, and other files for this article.
 |
Nakao Hayashi
Department of Mathematics,
Graduate School of Science
Osaka University, Osaka
Toyonaka, 560-0043, Japan
email: nhayashi@math.wani.osaka-u.ac.jp
|
|---|
 |
Pavel I. Naumkin
Instituto de Matemáticas
Universidad Nacional Autónoma de México
Campus Morelia, AP 61-3 (Xangari), Morelia CP 58089, Michoacán, Mexico
email: pavelni@matmor.unam.mx |
|---|
Return to the EJDE web page
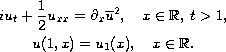
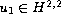 we prove
that there exists a unique global solution
we prove
that there exists a unique global solution
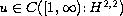 of this Cauchy
problem. Moreover we show that the large time asymptotic behavior
of the solution is defined in the region
of this Cauchy
problem. Moreover we show that the large time asymptotic behavior
of the solution is defined in the region
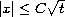 by the self-similar solution
by the self-similar solution
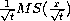 such that the total mass
such that the total mass
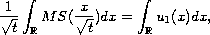
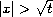 the asymptotic behavior of
solutions has rapidly oscillating structure similar to that of the cubic
nonlinear Schrodinger equations.
the asymptotic behavior of
solutions has rapidly oscillating structure similar to that of the cubic
nonlinear Schrodinger equations.

