Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 150, pp. 1-12.
Dispersive estimates for a linear wave equation with
electromagnetic potential
Davide Catania
Abstract:
We consider radial solutions to the Cauchy problem for a linear
wave equation with a small short-range electromagnetic potential
(depending on space and time) and zero initial data. We present
two dispersive estimates that provide, in particular, an optimal
decay rate in time
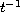 for the solution.
Also, we apply these estimates to obtain similar results for the
linear massless Dirac equation perturbed by a potential.
for the solution.
Also, we apply these estimates to obtain similar results for the
linear massless Dirac equation perturbed by a potential.
Submitted December 12, 2006. Published October 29, 2008.
Math Subject Classifications: 35A08, 35L05, 35L15, 58J37, 58J45.
Key Words: Wave equation; electromagnetic potential;
short-range; Dirac equation; dispersive estimate;
decay estimate.
Show me the
PDF file (239 KB),
TEX file for this article.
 |
Davide Catania
Dipartimento di Matematica, Facoltà di Ingegneria
Università di Brescia, Via Valotti 9, 25133 Brescia, Italy
email: catania@ing.unibs.it |
|---|
Return to the EJDE web page
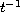 for the solution.
Also, we apply these estimates to obtain similar results for the
linear massless Dirac equation perturbed by a potential.
for the solution.
Also, we apply these estimates to obtain similar results for the
linear massless Dirac equation perturbed by a potential.
