Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 152, pp. 1-19.
Bifurcation and multiplicity results for a
nonhomogeneous semilinear elliptic problem
Kuan-Ju Chen
Abstract:
In this article we consider the problem

where
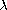 is a positive parameter.
We assume there exist
is a positive parameter.
We assume there exist
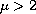 and
and
 such that
such that
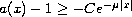 for all
for all
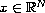 .
We prove that there exists a positive
.
We prove that there exists a positive
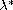 such that there are at least two positive solutions for
such that there are at least two positive solutions for
 and a unique positive solution for
and a unique positive solution for
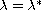 .
Also we show that
.
Also we show that
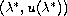 is a bifurcation point in
is a bifurcation point in
 .
.
Submitted May 13, 2008. Published November 04, 2008.
Math Subject Classifications: 35A15, 35J20, 35J25, 35J65.
Key Words: Nonhomogeneous semilinear elliptic problems; bifurcation.
Show me the
PDF file (315 KB),
TEX file for this article.
 |
Kuan-Ju Chen
Department of Applied Science, Naval Academy
P.O. BOX 90175 Zuoying, Taiwan
email: kuanju@mail.cna.edu.tw |
|---|
Return to the EJDE web page

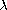 is a positive parameter.
We assume there exist
is a positive parameter.
We assume there exist
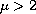 and
and
 such that
such that
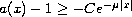 for all
for all
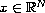 .
We prove that there exists a positive
.
We prove that there exists a positive
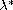 such that there are at least two positive solutions for
such that there are at least two positive solutions for
 and a unique positive solution for
and a unique positive solution for
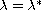 .
Also we show that
.
Also we show that
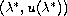 is a bifurcation point in
is a bifurcation point in
 .
.
