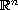 :
Necessary conditions for a constant configuration measure
:
Necessary conditions for a constant configuration measure
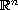 :
Necessary conditions for a constant configuration measure
:
Necessary conditions for a constant configuration measure
K. Zare
Abstract:
A formulation of the N-body problem is presented in which
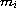 and
and
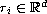 are the mass and the position vector of
the i-th body,
are the mass and the position vector of
the i-th body,
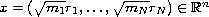 and
and
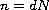 (
(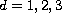 ).
The configuration measure
).
The configuration measure
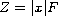 ,
where
,
where
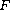 is the Poincare's force function,
which plays an important role in this formulation.
The orbit plane is a two dimensional linear subspace of
is the Poincare's force function,
which plays an important role in this formulation.
The orbit plane is a two dimensional linear subspace of
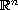 spanned by the position vector
spanned by the position vector
 and the velocity vector
and the velocity vector
 .
The N-body motion in
.
The N-body motion in
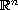 has been decomposed into an
orbit in the orbit plane and the instantaneous orientation of the
orbit plane. For a solution to stay on a level manifold of
has been decomposed into an
orbit in the orbit plane and the instantaneous orientation of the
orbit plane. For a solution to stay on a level manifold of
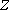 ,
it is necessary that the orbit in the orbit plane be elliptic
(
,
it is necessary that the orbit in the orbit plane be elliptic
( ),
parabolic
(
),
parabolic
(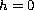 )
or hyperbolic
(
)
or hyperbolic
( )
where h is the total energy.
The instantaneous orientation of the orbit plane can be obtained by
integration of certain differential equations. These possible solutions
include the central configuration solutions in which the orbit plane is
fixed in
)
where h is the total energy.
The instantaneous orientation of the orbit plane can be obtained by
integration of certain differential equations. These possible solutions
include the central configuration solutions in which the orbit plane is
fixed in
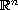 .
.
Submitted June 4, 2008. Published November 20, 2008.
Math Subject Classifications: 70F10.
Key Words: Configuration measure; Saari's conjecture; central configurations;
generalized vector product; generalized momentum and
eccentricity vectors.
Show me the PDF file (255 KB), TEX file for this article.
 |
Kal Zare Department of Mathematics Texas state University 601 University Drive San Marcos, TX 78666, USA email: kz11@txstate.edu |
|---|
Return to the EJDE web page