Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 24, pp. 1-15.
Growth rate and existence of solutions to Dirichlet problems for
prescribed mean curvature equations on unbounded domains
Zhiren Jin
Abstract:
We prove growth rate estimates and existence of solutions to
Dirichlet problems for prescribed mean curvature
equation on unbounded domains inside the complement
of a cone or a parabola like region in
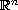 (
( ).
The existence results are proved using a modified Perron's
method by which a subsolution is a solution to the minimal
surface equation, while the role played by a supersolution is
replaced by estimates on the uniform
).
The existence results are proved using a modified Perron's
method by which a subsolution is a solution to the minimal
surface equation, while the role played by a supersolution is
replaced by estimates on the uniform
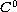 bounds on
the liftings of subfunctions on compact sets.
bounds on
the liftings of subfunctions on compact sets.
Submitted February 9, 2008. Published February 22, 2008.
Math Subject Classifications: 35J25, 35J60, 35J65.
Key Words: Elliptic boundary-value problem; quasilinear elliptic equation;
prescribed mean curvature equation; unbounded domain;
Perron's method
Show me the
PDF file (281 KB),
TEX file, and other files for this article.
 |
Zhiren Jin
Department of Mathematics and Statistics
Wichita State University
Wichita, Kansas 67260-0033, USA
email: zhiren@math.wichita.edu |
|---|
Return to the EJDE web page
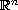 (
( ).
The existence results are proved using a modified Perron's
method by which a subsolution is a solution to the minimal
surface equation, while the role played by a supersolution is
replaced by estimates on the uniform
).
The existence results are proved using a modified Perron's
method by which a subsolution is a solution to the minimal
surface equation, while the role played by a supersolution is
replaced by estimates on the uniform
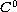 bounds on
the liftings of subfunctions on compact sets.
bounds on
the liftings of subfunctions on compact sets.
