We find sufficient conditions for the existence of global solutions for the systems of functional-differential equations
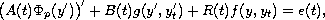
where
 which is the multidimensional p-Laplacian.
which is the multidimensional p-Laplacian.
Miroslav Bartusek, Milan Medved
Abstract:
We find sufficient conditions for the existence of global
solutions for the systems of functional-differential equations
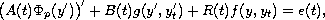
where
 which is the multidimensional p-Laplacian.
which is the multidimensional p-Laplacian.
Submitted January 29, 2008. Published March 20, 2008.
Math Subject Classifications: 34C11, 34K10.
Key Words: Second order functional-differential equation;
p-Laplacian; global solution.
Show me the PDF file (225 KB), TEX file for this article.
 |
Miroslav Bartusek Department of Mathematics and Statistics Faculty of Science, Masaryk University Janackovo nam. 2a, CZ-602 00 Brno, Czech Republic email: bartusek@math.muni.cz |
|---|---|
 |
Milan Medved Department of Mathematical Analysis and Numerical Mathematics Faculty of Mathematics, Physics and Informatics Comenius University, 842 48 Bratislava, Slovakia email: medved@fmph.uniba.sk |
Return to the EJDE web page