Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 44, pp. 1-9.
Non-monotone period functions for impact oscillators
Carmen Chicone, Kenny Felts
Abstract:
The existence of non-monotone period
functions for differential equations of the form
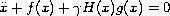
is proved for large
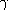 , where H is the Heaviside
function and the functions f and g satisfy certain
generic conditions. This result is precipitated by an
analysis of the system
, where H is the Heaviside
function and the functions f and g satisfy certain
generic conditions. This result is precipitated by an
analysis of the system
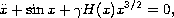
which models the conservative dimensionless impact pendulum
utilizing Hertzian contact during impact with a barrier at
the downward vertical position.
Submitted December 17, 2007. Published March 20, 2008.
Math Subject Classifications: 34C15, 34C25, 37N15.
Key Words: Period function; impact oscillator.
Show me the
PDF file (250 KB),
TEX file for this article.
 |
Carmen Chicone
Department of Mathematics
University of Missouri-Columbia
Columbia, MO 65211-4100, USA
e-mail: carmen@chicone.math.missouri.edu |
|---|
 |
Kenny Felts
Department of Mathematics
University of Missouri-Columbia
Columbia MO 65211-4100, USA
email: krf835@mizzou.edu |
|---|
Return to the EJDE web page
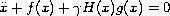
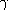 , where H is the Heaviside
function and the functions f and g satisfy certain
generic conditions. This result is precipitated by an
analysis of the system
, where H is the Heaviside
function and the functions f and g satisfy certain
generic conditions. This result is precipitated by an
analysis of the system