In this paper, we use the lower and upper solution method to obtain an existence theorem for the fourth-order boundary-value problem

where
![$f : [0,1]\times \mathbb{R}^4 \to \mathbb{R}$](gifs/ab.gif) ,
,
 are continuous and may be nonlinear, and
are continuous and may be nonlinear, and
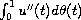 denotes the Riemann-Stieltjes integral.
denotes the Riemann-Stieltjes integral.
Yang Liu
Abstract:
In this paper, we use the lower and upper solution method to
obtain an existence theorem for the fourth-order
boundary-value problem

where
![$f : [0,1]\times \mathbb{R}^4 \to \mathbb{R}$](gifs/ab.gif) ,
,
 are continuous and may be nonlinear, and
are continuous and may be nonlinear, and
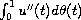 denotes the Riemann-Stieltjes integral.
denotes the Riemann-Stieltjes integral.
Submitted October 19, 2007. Published April 10, 2008.
Math Subject Classifications: 34B15.
Key Words: Fourth-order boundary-value problem; upper and lower solution;
Riemann-Stieltjies integral; Nagumo-type condition.
Show me the PDF file (192 KB), TEX file, and other files for this article.
 |
Yang Liu Department of Mathematics, Yanbian University Yanji, Jilin 133000, China. Department of Mathematics, Huaiyin Teachers College Huaian, Jiangsu 223300, China email: liuyang19830206@yahoo.com.cn |
|---|
Return to the EJDE web page