Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 56, pp. 1-16.
Existence of weak solutions for quasilinear elliptic equations
involving the p-Laplacian
Uberlandio Severo
Abstract:
This paper shows the existence of nontrivial weak
solutions for the quasilinear elliptic equation
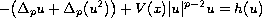
in
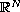 . Here
. Here
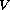 is a positive continuous
potential bounded away from zero and
is a positive continuous
potential bounded away from zero and
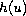 is a nonlinear term
of subcritical type.
Using minimax methods, we show the existence of a nontrivial solution
in
is a nonlinear term
of subcritical type.
Using minimax methods, we show the existence of a nontrivial solution
in
 and then show that it
decays to zero at infinity when
and then show that it
decays to zero at infinity when
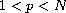 .
.
Submitted October 27, 2007. Published April 17, 2008.
Math Subject Classifications: 35J20, 35J60, 35Q55.
Key Words: Quasilinear Schrodinger equation; solitary waves;
p-Laplacian; variational method; mountain-pass theorem.
Show me the
PDF file (305 KB),
TEX file for this article.
 |
Uberlandio Severo
Departamento de Matemática,
Universidade Federal da Paraí ba
58051-900, João Pessoa, PB , Brazil
email: uberlandio@mat.ufpb.br Tel. 55 83 3216 7434
Fax 55 83 3216 7277 |
|---|
Return to the EJDE web page
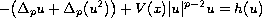
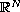 . Here
. Here
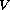 is a positive continuous
potential bounded away from zero and
is a positive continuous
potential bounded away from zero and
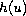 is a nonlinear term
of subcritical type.
Using minimax methods, we show the existence of a nontrivial solution
in
is a nonlinear term
of subcritical type.
Using minimax methods, we show the existence of a nontrivial solution
in
 and then show that it
decays to zero at infinity when
and then show that it
decays to zero at infinity when
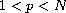 .
.
