In this note, we study the existence of a strong maximum principle for the nonlocal operator
 :=\int_{G}J(g)u(x*g^{-1})d\mu(g) - u(x),
$$](gifs/aa.gif)
where
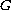 is a topological group acting continuously on a
Hausdorff space
is a topological group acting continuously on a
Hausdorff space
 and
and
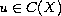 .
First we investigate the general situation and derive a pre-maximum
principle. Then we restrict our analysis to the case of homogeneous
spaces (i.e.,
.
First we investigate the general situation and derive a pre-maximum
principle. Then we restrict our analysis to the case of homogeneous
spaces (i.e.,
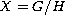 ).
For such Hausdorff spaces, depending
on the topology, we give a condition on
).
For such Hausdorff spaces, depending
on the topology, we give a condition on
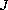 such that a strong
maximum principle holds for
such that a strong
maximum principle holds for
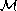 .
We also revisit the classical
case of the convolution operator (i.e.
.
We also revisit the classical
case of the convolution operator (i.e.
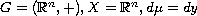 ).
).
