Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 78, pp. 1-13.
Boundary eigencurve problems involving
the p-Laplacian operator
Abdelouahed El Khalil, Mohammed Ouanan
Abstract:
In this paper, we show that for each
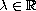 , there is
an increasing sequence of eigenvalues for the
nonlinear boundary-value problem
, there is
an increasing sequence of eigenvalues for the
nonlinear boundary-value problem
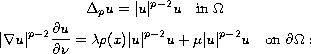
also we show that the first eigenvalue is simple and isolated.
Some results about their variation, density, and continuous
dependence on the parameter
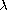 are obtained.
are obtained.
Editor's note:
After publication, we learned that this article is an unauthorized
copy of
"On the principal eigencurve of the p-Laplacian related to the
Sobolev trace embedding", Applicationes Mathematicae, 32, 1 (2005), 1-16.
The authors alone are responsible for this action which
may be in violation of the Copyright Laws.
Submitted September 16, 2007. Published May 27, 2008.
Math Subject Classifications: 35P30, 35J20, 35J60.
Key Words: p-Laplacian operator; nonlinear boundary conditions;
principal eigencurve; Sobolev trace embedding.
Show me the
PDF file (273 KB),
TEX file for this article.
 |
Abdelouahed El Khalil
Department of mathematics, College of Sciences
Al-Imam Muhammad Ibn Saud Islamic University
P. Box 90950, Riyadh 11623 Saudi Arabia
email: alakhalil@imamu.edu.sa lkhlil@hotmail.com
|
 |
Mohammed. Ouanan
University Moulay Ismail,
Faculty of Sciences et Technology
Department of informatics
P.O. Box 509, Boutalamine, 52000 Errachidia, Morocco
email: m_ouanan@hotmail.com |
Return to the EJDE web page
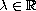 , there is
an increasing sequence of eigenvalues for the
nonlinear boundary-value problem
, there is
an increasing sequence of eigenvalues for the
nonlinear boundary-value problem
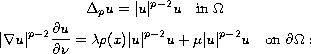
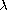 are obtained.
are obtained.

