Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 97, pp. 1-7.
Positivity of the Green functions for higher order
ordinary differential equations
Michael I. Gil'
Abstract:
We consider the equation
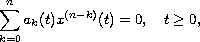
where
 ,
,
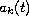 (
(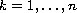 )
are real bounded functions.
Assuming that all the roots of the polynomial
)
are real bounded functions.
Assuming that all the roots of the polynomial
 (
(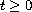 ) are real,
we derive positivity conditions for the Green function for the
Cauchy problem. We also establish
a lower estimate for the Green function
and a comparison theorem for solutions.
) are real,
we derive positivity conditions for the Green function for the
Cauchy problem. We also establish
a lower estimate for the Green function
and a comparison theorem for solutions.
Submitted May 8, 2008. Published July 25, 2008.
Math Subject Classifications: 34C10, 34A40.
Key Words: Linear ODE; Green function; fundamental solution;
positivity; comparison of solutions.
Show me the
PDF file (203 KB),
TEX file for this article.
 |
Michael I. Gil'
Department of Mathematics
Ben Gurion University of the Negev
P.0. Box 653, Beer-Sheva 84105, Israel
Email: gilmi@cs.bgu.ac.il |
|---|
Return to the EJDE web page
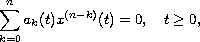
 ,
,
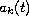 (
(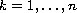 )
are real bounded functions.
Assuming that all the roots of the polynomial
)
are real bounded functions.
Assuming that all the roots of the polynomial
 (
(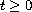 ) are real,
we derive positivity conditions for the Green function for the
Cauchy problem. We also establish
a lower estimate for the Green function
and a comparison theorem for solutions.
) are real,
we derive positivity conditions for the Green function for the
Cauchy problem. We also establish
a lower estimate for the Green function
and a comparison theorem for solutions.
