Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 113, pp. 1-26.
Homeomorphisms and Fredholm theory for perturbations of
nonlinear Fredholm maps of index zero with applications
Petronije S. Milojevic
Abstract:
We develop a nonlinear Fredholm alternative theory involving
k-ball and k-set perturbations of general homeomorphisms and
of homeomorphisms that are nonlinear Fredholm maps of index zero.
Various generalized first Fredholm theorems and finite
solvability of general (odd) Fredholm maps of index zero are also
studied. We apply these results to the unique and finite solvability
of potential and semilinear problems with strongly nonlinear boundary
conditions and to quasilinear elliptic equations. The basic tools
used are the Nussbaum degree and the degree theories for nonlinear
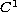 -Fredholm maps of index zero and their perturbations.
-Fredholm maps of index zero and their perturbations.
Submitted March 6, 2009. Published September 12, 2009.
Math Subject Classifications: 47H15, 35L70, 35L75, 35J40
Key Words: Nonlinear Fredholm mappings; index zero; homeomorphism;
Fredholm alternative; potential problems;
nonlinear boundary conditions; quasilinear elliptic equations.
Show me the PDF file (355 KB),
TEX file for this article.
 |
Petronije S. Milojevic
Department of Mathematical Sciences and CAMS
New Jersey Institute of Technology
Newark, NJ 07102, USA
email: milojevi@adm.njit.edu |
|---|
Return to the EJDE web page
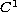 -Fredholm maps of index zero and their perturbations.
-Fredholm maps of index zero and their perturbations.
