We consider the regularity of weak solutions to the Navier-Stokes equations in
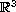 .
Let
.
Let
 be a weak
solution and
be a weak
solution and
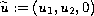 . We prove that
. We prove that
 is
strong solution if
is
strong solution if
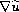 satisfy Serrin's type criterion.
satisfy Serrin's type criterion.
Jishan Fan, Hongjun Gao
Abstract:
We consider the regularity of weak solutions to the Navier-Stokes
equations in
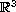 .
Let
.
Let
 be a weak
solution and
be a weak
solution and
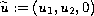 . We prove that
. We prove that
 is
strong solution if
is
strong solution if
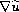 satisfy Serrin's type criterion.
satisfy Serrin's type criterion.
Submitted August 28, 2009. Published September 29, 2009.
Math Subject Classifications: 35Q30, 35K15, 76D03.
Key Words: Navier-Stokes equations; regularity criterion;
two component; multiplier spaces; Besov spaces.
Show me the PDF file (207 KB), TEX file for this article.
| Jishan Fan School of Mathematical Science, Nanjing Normal University, Nanjing, 210097, China Department of Applied Mathematics, Nanjing Forestry University, Nanjing 210037, China email: fanjishan@njfu.com.cn |
| Hongjun Gao School of Mathematical Science, Nanjing Normal University Nanjing, 210097, China email: gaohj@njnu.edu.cn |
Return to the EJDE web page