Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 141, pp. 1-15.
Precise asymptotic behavior of solutions to
damped simple pendulum equations
Tetsutaro Shibata
Abstract:
We consider the simple pendulum equation
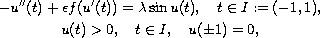
where
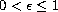 ,
,
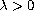 , and the friction term
is either
, and the friction term
is either
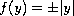 or
or
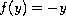 .
Note that when
.
Note that when
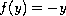 and
and
 , we have well known
original damped simple pendulum equation.
To understand the dependance of solutions, to the damped simple
pendulum equation with
, we have well known
original damped simple pendulum equation.
To understand the dependance of solutions, to the damped simple
pendulum equation with
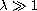 , upon the term
, upon the term
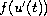 ,
we present asymptotic formulas for the maximum norm of the solutions.
Also we present an asymptotic formula for the time at which
maximum occurs, for the case
,
we present asymptotic formulas for the maximum norm of the solutions.
Also we present an asymptotic formula for the time at which
maximum occurs, for the case
 .
.
Submitted April 21, 2009. Published November 7, 2009.
Math Subject Classifications: 34B15.
Key Words: Damped simple pendulum; asymptotic formula.
Show me the PDF file (250 KB),
TEX file for this article.
 |
Tetsutaro Shibata
Department of Applied Mathematics, Graduate School of Engineering
Hiroshima University, Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
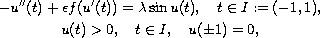
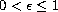 ,
,
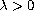 , and the friction term
is either
, and the friction term
is either
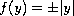 or
or
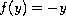 .
Note that when
.
Note that when
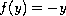 and
and
 , we have well known
original damped simple pendulum equation.
To understand the dependance of solutions, to the damped simple
pendulum equation with
, we have well known
original damped simple pendulum equation.
To understand the dependance of solutions, to the damped simple
pendulum equation with
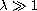 , upon the term
, upon the term
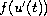 ,
we present asymptotic formulas for the maximum norm of the solutions.
Also we present an asymptotic formula for the time at which
maximum occurs, for the case
,
we present asymptotic formulas for the maximum norm of the solutions.
Also we present an asymptotic formula for the time at which
maximum occurs, for the case
 .
.
