Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 147, pp. 1-32.
Renormalized entropy solutions for degenerate nonlinear
evolution problems
Kaouther Ammar
Abstract:
We study the degenerate differential equation
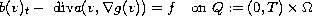
with the initial condition
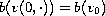 on
on
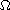 and
boundary condition
and
boundary condition
 on some part of the boundary
on some part of the boundary
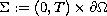 with
with
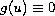 a.e. on
a.e. on
 .
The vector field
.
The vector field
 is
assumed to satisfy the Leray-Lions conditions, and the
functions
is
assumed to satisfy the Leray-Lions conditions, and the
functions
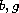 to be continuous, locally Lipschitz, nondecreasing
and to satisfy the normalization condition
to be continuous, locally Lipschitz, nondecreasing
and to satisfy the normalization condition
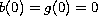 and the
range condition
and the
range condition
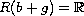 .
We assume also that
.
We assume also that
 has a flat region
has a flat region
![$[A_1,A_2]$](gifs/am.gif) with
with
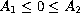 .
Using Kruzhkov's method of doubling
variables, we prove an existence and comparison result
for renormalized entropy solutions.
.
Using Kruzhkov's method of doubling
variables, we prove an existence and comparison result
for renormalized entropy solutions.
Submitted August 15, 2009. Published November 20, 2009.
Math Subject Classifications: 35K55, 35J65, 35J70, 35B30.
Key Words: Renormalized; degenerate; diffusion;
homogenous boundary conditions; continuous flux.
Show me the PDF file (373 KB),
TEX file, and other files for this article.
 |
Kaouther Ammar
TU Berlin, Institut für Mathematik, MA 6-3
Strasse des 17. Juni 136, 10623 Berlin, Germany
email: ammar@math.tu-berlin.de, Fax: +4931421110, Tel: +4931429306
|
|---|
Return to the EJDE web page
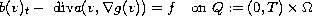
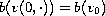 on
on
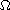 and
boundary condition
and
boundary condition
 on some part of the boundary
on some part of the boundary
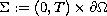 with
with
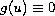 a.e. on
a.e. on
 .
The vector field
.
The vector field
 is
assumed to satisfy the Leray-Lions conditions, and the
functions
is
assumed to satisfy the Leray-Lions conditions, and the
functions
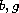 to be continuous, locally Lipschitz, nondecreasing
and to satisfy the normalization condition
to be continuous, locally Lipschitz, nondecreasing
and to satisfy the normalization condition
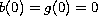 and the
range condition
and the
range condition
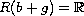 .
We assume also that
.
We assume also that
 has a flat region
has a flat region
![$[A_1,A_2]$](gifs/am.gif) with
with
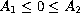 .
Using Kruzhkov's method of doubling
variables, we prove an existence and comparison result
for renormalized entropy solutions.
.
Using Kruzhkov's method of doubling
variables, we prove an existence and comparison result
for renormalized entropy solutions.
