Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 148, pp. 1-6.
A remark on the regularity for the 3D Navier-Stokes equations
in terms of the two components of the velocity
Sadek Gala
Abstract:
In this note, we study the regularity of Leray-Hopf weak solutions
to the Navier-Stokes equation, with the condition

where
 is the
Morrey-Campanato space for
is the
Morrey-Campanato space for
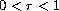 . Since
. Since

the above regularity condition allows us to improve the results
obtained by Fan and Gao [6].
Submitted November 5, 2009. Published November 25, 2009.
Math Subject Classifications: 35Q30, 35K15, 76D05.
Key Words: Navier-Stokes equations; regularity criterion;
Morrey-Campanato spaces.
Show me the PDF file (209 KB),
TEX file for this article.
Sadek Gala
Department of Mathematics, University of Mostaganem
Box 227, Mostaganem 27000, Algeria
email: sadek.gala@gmail.com
|
Return to the EJDE web page

 is the
Morrey-Campanato space for
is the
Morrey-Campanato space for
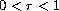 . Since
. Since
