In this paper, we obtain Liapunov-type integral inequalities for certain nonlinear, nonhomogeneous differential equations of higher order with without any restriction on the zeros of their higher-order derivatives of the solutions by using elementary analysis. As an applications of our results, we show that oscillatory solutions of the equation converge to zero as
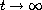 .
Using these inequalities, it is also shown that
.
Using these inequalities, it is also shown that
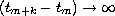 as
as
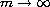 ,
where
,
where
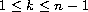 and
and
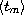 is an
increasing sequence of zeros of an oscillatory solution of
is an
increasing sequence of zeros of an oscillatory solution of
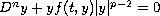 ,
,
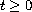 ,
provided that
,
provided that
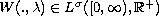 ,
,
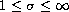 and for all
and for all
 .
A criterion for
disconjugacy of nonlinear homogeneous equation is obtained in an
interval
.
A criterion for
disconjugacy of nonlinear homogeneous equation is obtained in an
interval
![$[a, b]$](gifs/ak.gif) .
.
