 on a domain with a corner
on a domain with a corner
 on a domain with a corner
on a domain with a corner
Tymofiy Gerasimov, Guido Sweers
Abstract:
The operator
 appears in a model for the
vertical displacement of a two-dimensional grid that consists of
two perpendicular sets of elastic fibers or rods. We are interested
in the behaviour of such a grid that is clamped at the boundary and
more specifically near a corner of the domain.
Kondratiev supplied the appropriate setting in the sense of Sobolev
type spaces tailored to find the optimal regularity. Inspired by
the Laplacian and the Bilaplacian models one expect, except maybe for
some special angles that the optimal regularity improves when angle
decreases. For the homogeneous Dirichlet problem with this special
non-isotropic fourth order operator such a result does not hold true.
We will show the existence of an interval
appears in a model for the
vertical displacement of a two-dimensional grid that consists of
two perpendicular sets of elastic fibers or rods. We are interested
in the behaviour of such a grid that is clamped at the boundary and
more specifically near a corner of the domain.
Kondratiev supplied the appropriate setting in the sense of Sobolev
type spaces tailored to find the optimal regularity. Inspired by
the Laplacian and the Bilaplacian models one expect, except maybe for
some special angles that the optimal regularity improves when angle
decreases. For the homogeneous Dirichlet problem with this special
non-isotropic fourth order operator such a result does not hold true.
We will show the existence of an interval
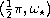 ,
,
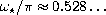 (in degrees
(in degrees
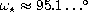 ),
in which the optimal regularity improves with increasing opening angle.
),
in which the optimal regularity improves with increasing opening angle.
Submitted December 10, 2008. Published April 2, 2009.
Math Subject Classifications: 35J40, 46E35, 35P30.
Key Words: Nonisotropic; fourth order PDE; domain with corner;
clamped grid; weighted Sobolev space; regularity.
Show me the PDF file (941 KB), TEX file for this article.
 |
Tymofiy Gerasimov DIAM-EWI, Delft University of Technology PO box 5031, 2600 GA Delft, The Netherlands email: t.gerasimov@tudelft.nl |
|---|---|
 |
Guido Sweers MI, Universität zu Köln D 50931 Cologne, Germany email: gsweers@math.uni-koeln.de |
Return to the EJDE web page