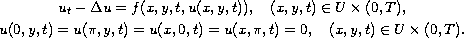Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 77, pp. 1-13.
Remarks on a 2-D nonlinear backward heat problem
using a truncated Fourier series method
Dang Duc Trong, Nguyen Huy Tuan
Abstract:
The inverse conduction problem arises when experimental measurements
are taken in the interior of a body, and it is desired to calculate
temperature on the surface. We consider the problem of finding,
from the final data
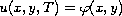 , the initial data
, the initial data
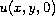 of the temperature function
of the temperature function
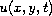 ,
,
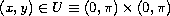 ,
,
![$t\in [0,T]$](gifs/ae.gif) satisfying the nonlinear system
satisfying the nonlinear system
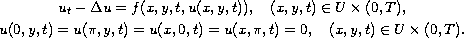
This problem is known to be ill-posed, as the solution exhibits
unstable dependence on the given data functions.
Using the Fourier series method, we regularize the problem and
to get some new error estimates.
A numerical experiment is given.
Submitted December 11, 2008. Published June 16, 2009.
Math Subject Classifications: 35K05, 35K99, 47J06, 47H10.
Key Words: Backward heat problem; nonlinearly ill-posed problem;
Fourier series; contraction principle.
Show me the PDF file (249 KB),
TEX file, and other files for this article.
 |
Dang Duc Trong
Department of Mathematics and Informatics
Hochiminh City National University
227 Nguyen Van Cu, Q. 5, Hochiminh City, Vietnam
email: ddtrong@mathdep.hcmuns.edu.vn |
|---|
 |
Nguyen Huy Tuan
Department of Information Technology and Mathematics
Ton Duc Thang University
98 Ngo Tat To, Hochiminh City, Vietnam
email: tuanhuy_bs@yahoo.com |
|---|
Return to the EJDE web page
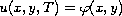 , the initial data
, the initial data
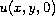 of the temperature function
of the temperature function
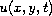 ,
,
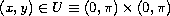 ,
,
![$t\in [0,T]$](gifs/ae.gif) satisfying the nonlinear system
satisfying the nonlinear system