For the focusing mass-critical nonlinear Schrodinger equation
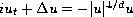 , an important problem is to
establish Liouville type results for solutions with ground state mass.
Here the ground state is the positive solution to elliptic equation
, an important problem is to
establish Liouville type results for solutions with ground state mass.
Here the ground state is the positive solution to elliptic equation
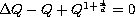 .
Previous results in this direction were established in
[12, 16, 17, 29] and they all require
.
Previous results in this direction were established in
[12, 16, 17, 29] and they all require
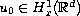 . In this paper, we consider
the rigidity results for rough initial data
. In this paper, we consider
the rigidity results for rough initial data
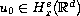 for any
for any
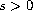 .
We show that in dimensions
.
We show that in dimensions
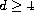 and under the radial assumption,
the only solution that does not scatter in both time directions
(including the finite time blowup case) must be global and coincide
with the solitary wave
and under the radial assumption,
the only solution that does not scatter in both time directions
(including the finite time blowup case) must be global and coincide
with the solitary wave
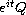 up to symmetries of the equation.
The proof relies on a non-uniform local iteration scheme, the refined
estimate involving the
up to symmetries of the equation.
The proof relies on a non-uniform local iteration scheme, the refined
estimate involving the
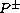 operator and a new smoothing estimate
for spherically symmetric solutions.
operator and a new smoothing estimate
for spherically symmetric solutions.