We study the existence of nontrivial solutions to the boundary-value problem
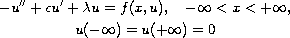
and to the system
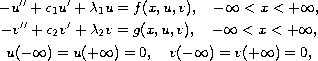
where
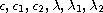 are real
positive constants and the nonlinearities
are real
positive constants and the nonlinearities
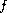 and
and
 satisfy
suitable conditions.
The proofs are based on fixed point theorems.
satisfy
suitable conditions.
The proofs are based on fixed point theorems.
Toufik Moussaoui, Radu Precup
Abstract:
We study the existence of nontrivial solutions to the
boundary-value problem
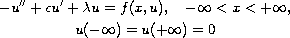
and to the system
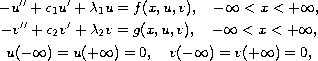
where
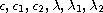 are real
positive constants and the nonlinearities
are real
positive constants and the nonlinearities
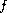 and
and
 satisfy
suitable conditions.
The proofs are based on fixed point theorems.
satisfy
suitable conditions.
The proofs are based on fixed point theorems.
Submitted October 7, 2008. Published August 6, 2009.
Math Subject Classifications: 34B40.
Key Words: Boundary value problem; fixed point theorem.
Show me the PDF file (227 KB), TEX file for this article.
 |
Toufik Moussaoui Department of Mathematics, E.N.S. P.O. Box 92, 16050 Kouba, Algiers, Algeria email: moussaoui@ens-kouba.dz |
|---|---|
 |
Radu Precup Department of Applied Mathematics Babes-Bolyai University 400084 Cluj, Romania e-mail: r.precup@math.ubbcluj.ro |
Return to the EJDE web page