Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 98, pp. 1-10.
Existence of positive solutions for a fourth-order
multi-point beam problem on measure chains
Douglas R. Anderson, Feliz Minhos
Abstract:
This article concerns the fourth-order multi-point beam problem
![$$\displaylines{
(EIW^{\Delta \nabla }) ^{\nabla \Delta }(x)=m(x)f(x,W(x)),\quad
x\in [x_{1},x_{n}]_{\mathbb{X}} \cr
W(\rho ^2(x_{1}))=\sum_{i=2}^{n-1}a_iW(x_i),\quad
W^{\Delta}(\rho ^2(x_{1}))=0, \cr
(EIW^{\Delta \nabla }) (\sigma (x_{n}))=0,\quad
(EIW^{\Delta \nabla })^{\nabla }(\sigma(x_{n}))
=\sum_{i=2}^{n-1}b_i(EIW^{\Delta \nabla })^{\nabla}(x_i).
}$$](gifs/aa.gif)
Under various assumptions on the functions
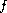 and
and
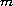 and the coefficients
and the coefficients
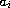 and
and
 we establish the existence of one or two positive solutions
for this measure chain boundary value problem using the
Green's function approach.
we establish the existence of one or two positive solutions
for this measure chain boundary value problem using the
Green's function approach.
Submitted February 6, 2009. Published August 11, 2009.
Math Subject Classifications: 34B15, 39A10.
Key Words: Measure chains; boundary value problems; Green's function;
fixed point; fourth order; cantilever beam.
Show me the PDF file (254 KB),
TEX file for this article.
 |
Douglas R. Anderson
Department of Mathematics, Concordia College
Moorhead, MN 56562 USA
email: andersod@cord.edu
|
|---|
 |
Feliz Minhós
Department of Mathematics
University of Évora, Portugal
email: fminhos@uevora.pt
|
|---|
Return to the EJDE web page
![$$\displaylines{
(EIW^{\Delta \nabla }) ^{\nabla \Delta }(x)=m(x)f(x,W(x)),\quad
x\in [x_{1},x_{n}]_{\mathbb{X}} \cr
W(\rho ^2(x_{1}))=\sum_{i=2}^{n-1}a_iW(x_i),\quad
W^{\Delta}(\rho ^2(x_{1}))=0, \cr
(EIW^{\Delta \nabla }) (\sigma (x_{n}))=0,\quad
(EIW^{\Delta \nabla })^{\nabla }(\sigma(x_{n}))
=\sum_{i=2}^{n-1}b_i(EIW^{\Delta \nabla })^{\nabla}(x_i).
}$$](gifs/aa.gif)
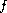 and
and
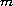 and the coefficients
and the coefficients
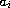 and
and
 we establish the existence of one or two positive solutions
for this measure chain boundary value problem using the
Green's function approach.
we establish the existence of one or two positive solutions
for this measure chain boundary value problem using the
Green's function approach.

