This article concerns the existence of solutions and the decay of the energy of the mixed problem for the coupled system of Klein-Gordon equations

with the nonlinear boundary conditions,
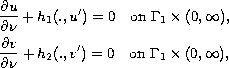
and boundary conditions
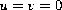 on
on
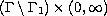 , where
, where
 is a bounded open set of
is a bounded open set of
 ,
,
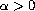 a real number,
a real number,
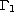 a subset of the boundary
a subset of the boundary
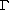 of
of
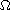 and
and
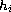 a real function defined on
a real function defined on
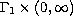 .
Assuming that each
.
Assuming that each
 is strongly monotone in the second
variable, the existence of global solutions of the mixed problem
is obtained. For that it is used the Galerkin method, the Strauss'
approximations of real functions and trace theorems for non-smooth
functions. The exponential decay of the energy for a particular
stabilizer is derived by application of a Lyapunov functional.
is strongly monotone in the second
variable, the existence of global solutions of the mixed problem
is obtained. For that it is used the Galerkin method, the Strauss'
approximations of real functions and trace theorems for non-smooth
functions. The exponential decay of the energy for a particular
stabilizer is derived by application of a Lyapunov functional.

