Electron. J. Diff. Equ., Vol. 2010(2010), No. 153, pp. 1-7.

Regularity for 3D Navier-Stokes equations in terms of two components of the vorticity

Sadek Gala

Abstract:
We establish regularity conditions for the 3D Navier-Stokes equation via two components of the vorticity vector. It is known that if a Leray-Hopf weak solution $u$ satisfies
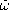$$ \tilde{\omega}\in L^{2/(2-r)}(0,T;L^{3/r}(\mathbb{R}^3))\quad \hbox{with }0<r<1, $$
where $\tilde{\omega}$ form the two components of the vorticity, 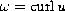$\omega =\operatorname{curl}u$, then $u$ becomes the classical solution on $(0,T]$ (see [5]). We prove the regularity of Leray-Hopf weak solution $u$ under each of the following two (weaker) conditions:
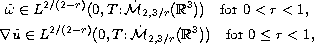
$$\displaylines{ \tilde{\omega}\in L^{2/(2-r)}(0,T;\dot {\mathcal{M}}_{2, 3/r}(\mathbb{R}^3))\quad \hbox{for }0<r<1,\cr \nabla \tilde{u}\in L^{2/(2-r)}(0,T;\dot {\mathcal{M}}_{2, 3/r}(\mathbb{R}^3))\quad \hbox{for }0\leq r<1, }$$
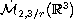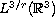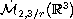where $\dot {\mathcal{M}}_{2,3/r}(\mathbb{R}^3)$ is the Morrey-Campanato space. Since $L^{3/r}(\mathbb{R}^3)$ is a proper subspace of $\dot {\mathcal{M}}_{2,3/r}(\mathbb{R}^3)$, our regularity criterion improves the results in Chae-Choe [5].

Submitted May 20, 2010. Published October 28, 2010.
Math Subject Classifications: 35Q35, 76C99.
Key Words: Navier-Stokes equations; regularity conditions; Morrey-Campaanto spaces.

Show me the PDF file (219 KB), TEX file for this article.

Sadek Gala
Department of Mathematics, University of Mostaganem
Box 227, Mostaganem 27000, Algeria
email: sadek.gala@gmail.com

Return to the EJDE web page