Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 23, pp. 1-10.
Oscillation of solutions for odd-order
neutral functional differential equations
Tuncay Candan
Abstract:
In this article, we establish oscillation criteria
for all solutions to the neutral differential equations
![$$
[x(t)\pm ax(t\pm h)\pm bx(t\pm g)]^{(n)}
=p\int_{c}^{d}x(t-\xi)d\xi+q\int_{c}^{d}x(t+\xi)d\xi,
$$](gifs/aa.gif)
where
 is odd,
is odd,
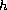 ,
,
 ,
,
 and
and
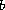 are nonnegative
constants. We consider 10 of the 16 possible combinations
of +/- signs, and give some examples to illustrate our results.
are nonnegative
constants. We consider 10 of the 16 possible combinations
of +/- signs, and give some examples to illustrate our results.
Submitted December 9, 2009. Published February 4, 2010.
Math Subject Classifications: 34K11, 34K40.
Key Words: Neutral differential equations; oscillation of solutions;
distributed deviating arguments.
Show me the PDF file (204 KB),
TEX file for this article.
 |
Tuncay Candan
Department of Mathematics,
Faculty of Art and Science
Nigde University, Nigde, 51200, Turkey
email: tcandan@nigde.edu.tr
|
|---|
Return to the EJDE web page
![$$
[x(t)\pm ax(t\pm h)\pm bx(t\pm g)]^{(n)}
=p\int_{c}^{d}x(t-\xi)d\xi+q\int_{c}^{d}x(t+\xi)d\xi,
$$](gifs/aa.gif)
 is odd,
is odd,
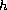 ,
,
 ,
,
 and
and
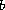 are nonnegative
constants. We consider 10 of the 16 possible combinations
of +/- signs, and give some examples to illustrate our results.
are nonnegative
constants. We consider 10 of the 16 possible combinations
of +/- signs, and give some examples to illustrate our results.
