Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 25, pp. 1-14.
Parabolic equations with Robin type boundary conditions
in a non-rectangular domain
Arezki Kheloufi, Boubaker-Khaled Sadallah
Abstract:
In this article, we study the parabolic equation
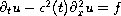 in the non-necessarily rectangular domain
in the non-necessarily rectangular domain

The boundary conditions are of Robin type, while the right-hand
side lies in the Lebesgue space
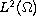 .
Our aim is to find conditions on
.
Our aim is to find conditions on
 and the functions
and the functions
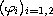 such that the solution
belongs to the anisotropic Sobolev space
such that the solution
belongs to the anisotropic Sobolev space
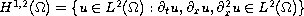 .
For goal we use the method of approximation of domains.
.
For goal we use the method of approximation of domains.
Submitted July 29, 2009. Published February 10, 2010.
Math Subject Classifications: 35K05, 35K20.
Key Words: Parabolic equation; non-rectangular domains;
Robin condition; anisotropic Sobolev space.
Show me the PDF file (264 KB),
TEX file, and other files for this article.
 |
Arezki Kheloufi
Department of Sciences and Techniques, Faculty of Technology
Béjaia University, 6000. Béjaia, Algeria
email: arezkinet2000@yahoo.fr
|
|---|
 |
Boubaker-Khaled Sadallah
Department of Mathematics, E.N.S.
16050 Kouba. Algiers, Algeria
email: sadallah@ens-kouba.dz
|
|---|
Return to the EJDE web page
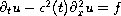 in the non-necessarily rectangular domain
in the non-necessarily rectangular domain

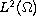 .
Our aim is to find conditions on
.
Our aim is to find conditions on
 and the functions
and the functions
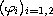 such that the solution
belongs to the anisotropic Sobolev space
such that the solution
belongs to the anisotropic Sobolev space
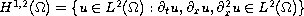 .
For goal we use the method of approximation of domains.
.
For goal we use the method of approximation of domains.

